Leetcode 2331 - Evaluate Boolean Binary Tree

Problem Description

You are given the root of a full binary tree with the following properties:

• Leaf nodes have either the value 0 or 1, where 0 represents False and 1 represents True.
• Non-leaf nodes have either the value 2 or 3, where 2 represents the boolean OR and 3 represents the boolean AND.

The evaluation of a node is as follows:

If the node is a leaf node, the evaluation is the value of the node, i.e. True or False. Otherwise, evaluate the node's two children and apply the boolean operation of its value with the children's evaluations. Return the boolean result of evaluating the root node.

A full binary tree is a binary tree where each node has either 0 or 2 children.

A leaf node is a node that has zero children.

Examples

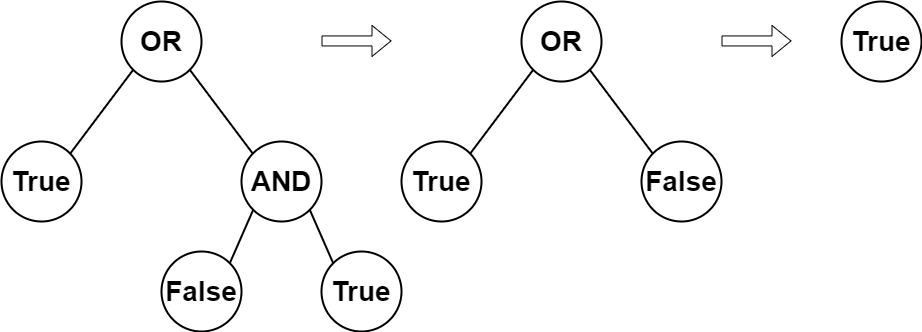
Input: root = [2,1,3,null,null,0,1]

Output: true

Explanation: The above diagram illustrates the evaluation process. The AND node evaluates to False AND True = False. The OR node evaluates to True OR False = True. The root node evaluates to True, so we return true.

Thought Process / Intuition

A binary tree question, asking us to return a boolean value after evaluating the tree. I imagine the evaluation process as nodes combining from bottom up towards the root node and finally returning a boolean value. This can be done through recursion, where the return value is the information needed to be passed to the parent nodes. Then we just have to employ some checks for the node's value to run either or or and and return that value, and with wishful thinking and recursion we can arrive at the final answer.

Approach

1. We define a recursive function dfs that takes a node as input and returns a boolean value.
2. If the node is a leaf node, we return the True or False depending on the value of the node.
3. Otherwise, we recursively evaluate the left and right children of the node.
4. If the node's value is 2, we return the logical OR of the evaluations of the left and right children.
5. If the node's value is 3, we return the logical AND of the evaluations of the left and right children.
6. We call the dfs function on the root node and return the result.

Solution

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def evaluateTree(self, root: Optional[TreeNode]) -> bool:
        def dfs(root):
            #is_leaf check
            if root.left is None and root.right is None:
                if root.val == 0:
                    return False
                return True
            left = dfs(root.left)
            right = dfs(root.right)
            if root.val == 2:
                return left or right
            if root.val == 3:
                return left and right
        return dfs(root)
            

Complexity Analysis

Time complexity: $O(n)$

• The time complexity of the solution is $O(n)$, where $n$ is the number of nodes in the binary tree.
• We visit each node once in the binary tree during the recursive traversal.
• Thus, the time complexity of the recursive function dfs is $O(n)$.

Space complexity: $O(log n)$

• The space complexity of the solution is $O(log n)$.
• The recursive call stack of the solution is proportional to the height of the binary tree. Since the binary tree is a full binary tree, the height of the tree is $log n$. Thus, the space complexity is $O(log n)$.

Shoutout to My Friends' Solutions on Leetcode

My Solution